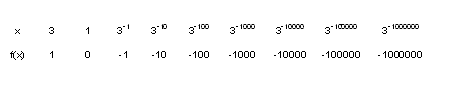Gráficas de funciones logarítmicas

        Tutorial paso a paso. Las propiedades tales como dominio, rango, asíntotas verticales y las intersecciones de las gráficas de estas funciones también se examinan en detalles.

Revisar

        En primer lugar, comenzar con las propiedades de la gráfica de la función logarítmica de base de una base,

f (x) = log _a(x), a > 0 y no es igual a 1.

        El dominio de la función f es el intervalo (0, + inf). El rango de f es el intervalo (-inf, + inf).

La inf símbolo significa infinito.

        La función f tiene una asíntota vertical dada por x = 0. Esta función tiene una x en la intersección (1, 0). f aumenta a medida que aumenta x.

Ejemplo 1:

f es una función dada por

f (x) = log ₂ (x + 2)

a - Determine el dominio de f y el rango de f.
b - Encuentra la asíntota vertical de la gráfica de f.
c - Encuentra la X y la intercepta y de la gráfica de f si los hay.
d - Dibuje la gráfica de f.

Respuesta al Ejemplo 1

a - El dominio de f es el conjunto de todos los valores de x tal que 

x + 2 > 0

x > -2

El rango de f es el intervalo (-inf, + inf).

b - La asíntota vertical se obtiene mediante la solución de

 x + 2 = 0

lo que da

 x = -2

        Cuando x tiende a -2 de la derecha (x> -2), f (x) decrece sin límite. ¿Cómo sabemos esto?

Veamos algunos valores:

f (-1) = log ₂ (-1 + 2) = log ₂ (1) = 0

f (-1,5) = log ₂ (-1,5 + 2) = log ₂ (1 / 2) = -1

f (-1,99) = log ₂ (-1,99 + 2) = log ₂ (0.01), que es aproximadamente igual a -6,64

f (-1.999999) = log ₂ (-1,999999 + 2) = log ₂ (0.000001), que es aproximadamente igual a -19,93.

c - Para encontrar la intersección x tenemos que resolver la ecuación f (x) = 0

log₂ (x + 2) = 0

        Usar las propiedades de las funciones logarítmicas y exponenciales para escribir la ecuación anterior como

 x + 2 = 2^0

x = -1

La intersección x es (-1, 0).

La intersección está dada por (0, f (0)) = (0, log ₂ (0 + 2)) = (0, 1).

d - Hasta ahora tenemos el dominio, rango, x e intercepta y, y la asíntota vertical. Necesitamos más puntos. Vamos a considerar un punto en x = -3 / 2 (a medio camino entre la X y la intersección de la asíntota vertical) y otro punto en x = 2.

f (-3 / 2) = log ₂ (-3 / 2 + 2) = log ₂ (1 / 2) = log ₂ (2 ^-1) = -1.

f (2) = log ₂ (2 + 2) = log ₂ (2 ²) = 2.

        Ahora tenemos más información sobre la forma de gráfico de f. El gráfico aumenta a medida que aumenta x. Cerca de la asíntota vertical x = -2, la gráfica de f disminuye sin límite cuando x tiende a -2 de la derecha. La gráfica no corta la asíntota vertical. Nos unen ahora a los diferentes puntos de una curva suave.

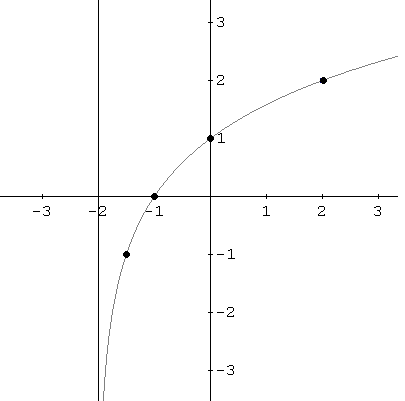
Ejemplo 2:

f es una función dada por

a - f (x) = -3ln (x - 4)

b - Determine el dominio de f y el rango de f.

c - Encuentra la asíntota vertical de la gráfica de f.

d - Encuentra la X y la intercepta y de la gráfica de f si los hay.

e - Dibuje la gráfica de f.

Respuesta al Ejemplo 2

a - El dominio de f es el conjunto de todos los valores de x tal que 

x - 4 > 0

x > 4

El rango de f es el intervalo (-inf, + inf).

b - La asíntota vertical se obtiene mediante la solución de

 x - 4 = 0

x = 4

        Cuando x tiende a 4 de la derecha (x> 4), f (x) crece sin límite. ¿Cómo sabemos esto?

Veamos algunos valores:

f (5) = ln (5-4) =-3ln (1) = 0

f (4,001) =-3ln (0,001), que es aproximadamente igual a 20,72.

f (4.000001) =-3ln (0,000001), que es aproximadamente igual a 41,45.

c - Para encontrar la intersección x tenemos que resolver la ecuación f (x) = 0

-3ln(x - 4) = 0

Divide ambos lados por -3 a obtener

ln (x - 4) = 0

        Usar las propiedades de las funciones logarítmicas y exponenciales para escribir la ecuación anterior como

e ^{ln (x - 4)} = e ⁰

Luego de simplificar

 x - 4 = 1

x = 5

La x es interceptar en (5, 0).

        La intersección está dada por (0, f (0)). f (0) no está definido ya que x = 0 no es un valor en el dominio de f. No hay ninguna intersección.

d - Hasta ahora tenemos el dominio, rango, x interceptar y la asíntota vertical. Necesitamos puntos extra para poder gráfico de f.

f (4,5) =-3ln (4,5 - 4) aproximadamente igual a 2,08

F (8) =-3ln (8 - 4) aproximadamente igual a - 4,16

f (14) =-3ln (14 - 4) aproximadamente igual a - 6,91

        Veamos ahora esbozar todos los puntos y la asíntota vertical. Únete a los puntos por una curva suave y F aumenta a medida que x se aproxima a 4 de la derecha.

Ejemplo 3:

f es una función dada por

f (x) = 2ln (| X |)

a - Determine el dominio de f y el rango de f.

b - Encuentra la asíntota vertical de la gráfica de f.

c - Encuentra la X y la intercepta y de la gráfica de f si los hay.

d - Dibuje la gráfica de f.

Respuesta al Ejemplo 3

a - El dominio de f es el conjunto de todos los valores de x tal que

|x| > 0

El dominio es el conjunto de todos los números reales excepto 0.

El rango de f es el intervalo (-inf, + inf).

b - La asíntota vertical se obtiene mediante la solución de

|x| = 0

lo que da

x = 0

        Cuando x tiende a 0 por la derecha (x> 0), f (x) decrece sin límite. ¿Cómo sabemos esto?

Veamos algunos valores:

f (1) = 2 ln (| 1 |) = 0
f (0,1) = 2ln (0,1), que es aproximadamente igual a -4,61.

f (0,0001) = 2ln (0,0001), que es aproximadamente igual a -18,42.

f (0.0000001) = 2ln (0,0000001), que es aproximadamente igual a -32,24.

        Cuando x se aproxima a 0 por la izquierda (x <0), f (x) decrece sin límite. ¿Cómo sabemos esto?

Veamos algunos valores:

f (-1) = 2 ln (| -1 |) = 0

f (-0,1) = 2ln (| -0,1 |), que es aproximadamente igual a -4,61.

f (-0,0001) = 2ln (| -0,0001 |), que es aproximadamente igual a -18,42.

f (-0.0000001) = 2ln (| -0,0000001 |), que es aproximadamente igual a -32,24.

c - Para encontrar la intersección x tenemos que resolver la ecuación f (x) = 0

2ln (| X |) = 0

Divide ambos lados por 2 para obtener

ln (| X |) = 0

        Usar las propiedades de las funciones logarítmicas y exponenciales para escribir la ecuación anterior como

e ^{ln (| X |)} = e ⁰

Luego de simplificar

 | X | = 1

Dos x intercepta en (1, 0) y (-1, 0).

        La intersección está dada por (0, f (0)). f (0) no está definido ya que x = 0 no es un valor en el dominio de f. No hay ninguna intersección.

d - Hasta ahora tenemos el dominio, rango, x interceptar y la asíntota vertical. Mediante el examen de la función f es fácil demostrar que esta es una función par y su gráfica es simétrica con respecto al eje y.

f (-x) = 2 ln (|-x |)

pero

|-x | = | x |

y por lo tanto

f (-x) = 2 ln (| x |) = f (x), esto demuestra que f es una función par.

Vamos a encontrar puntos extra.

f (4) = 2ln (| 4 |) aproximadamente igual a 2,77.

f (0,5) = 2ln (| 0.5 |) aproximadamente igual a - 1,39.

Como f es aún f (-4) = f (4) y f (-0,5) = f (0,5).

        Veamos ahora esbozar todos los puntos, la asíntota vertical y Una los puntos por una curva suave.

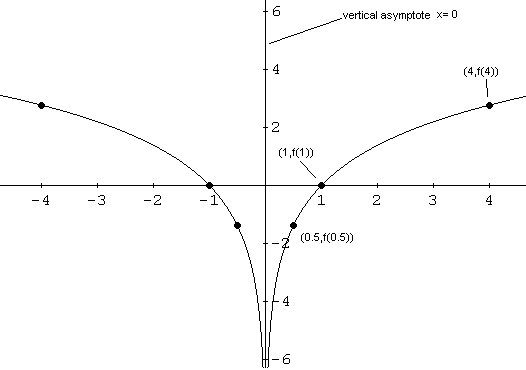
Informacion obtenida de: http://www.analyzemath.com/spanish/Graphing/GraphLogarithmicFunction.html

Videos - Manejo y procedimiento de fun. Logaritmicas

Manejos y procedimientos de las funciones logaritmicas - 3 partes

Ejemplos de procedimiento y grafica

Teoria y practica - 2 partes

Parte 1

Parte 2

Vertical asíntota de la función logarítmica

        Log _B 0 es indefinido. Sin embargo, es posible investigar el comportamiento de la gráfica de la función logarítmica a medida que x se acerca a cero por la derecha (x> 0).

Ejemplo

        Sea f (x) = log ₃ x, y encontrar los valores de f (x) cuando x se aproxima a cero. Los resultados se muestran en el cuadro siguiente.

 

        Cuando x se acerca a cero, f (x) decrece sin límite. En el gráfico se acerca al eje y (x = 0). La línea vertical x = 0 se denomina a la asíntota vertical.

Informacion obtenida de: http://www.analyzemath.com/spanish/logfunction/logfunction.html

Logaritmos Comunes y Naturales

Hoy en dia utilizamos una calculadora para elevar los logaritmos con base 10 para los logaritmos comunes y con base e para los logaritmos naturales.

Logaritmos Comunes

El logaritmo con base 10 se conoce como logaritmo común y se denota omitiendo la base:

log x=
 

A partir de la definicion de logaritmo determinamos que

log 10 = 1     y     log 100 = 2

Logaritmos Naturales

El logaritmo con base e se conoce como logaritmo natural y se denota por Ln

ln x =
 

La funcion logaritmo natural y=ln x es la funcion inversa de la funcion exponencial y= ex.

                    

ln x = y

       
Informacion obtenida de:

http://www.wikimatematica.org/index.php?title=Funciones_Logar%C3%ADtmicas#Logaritmos_Comunes_y_Naturales

Historia y Propiedades

 Historia

        Historicamente, los exponentes fueron introducidos en matemáticas para dar un método corto que indicara el producto de varios factores semejantes, y, con este propósito, solo se consideraron inicialmente exponentes naturales. 

        La noción de progresión geométrica no es nueva en Matemática. Existe evidencia que muestra que los egipcios y babilonios manejaban este concepto, y desde luego también los griegos. En Los elementos de Euclides aparece un enunciado que establece la igualdad

a^m+n = a^maⁿ

para n y m enteros positivos.

        Ya en la Edad Media, N. Oresme (francés, s. XIV) vuelve a hallar esta regla, hablando de exponentes racionales, y estableciendo otras identidades como

(ab)^1/n = a^1/nb^1/n

        Sus ideas, muy avanzadas para la época, no fueron entendidas, y un siglo después N. Choquet las retoma, introduciendo además exponentes enteros no positivos. En esta época se consolida la función exponencial (no conocida como tal) como isomorfismo entre los números reales (no conocidos como tales). En el siglo XVI, el matemático alemán Stifel completó el trabajo, introduciendo exponentes racionales arbitrarios, y el paso a exponentes reales fue realizado por J. Neper2.1 (o Napier) y J. Bürgi entre 1614 y 1620, de manera intuitiva. Desde entonces, y hasta mediados del siglo XIX, se admitió esta manera intuitiva de pasar a exponentes reales, al no disponerse de una teoría sólida de números reales que permitiera hacerlo más rigurosamente.

        Aunque hoy en día se enseñan a veces como un tema aislado, lo cierto es que los logaritmos (y por ende, las potencias) aparecieron como una herramienta de cálculo. En efecto, al parecer ya Arquímedes utilizaba la idea de reducir la multiplicación de dos números (potencias de 2, por ejemplo), por medio de la suma de sus logaritmos. Pero el verdadero auge de los logaritmos, como herramienta de cálculo, sobre todo en navegación, finanzas y cálculos astronómicos, comienza en el siglo XVI con Stifel, y se consolida a inicios del XVII con Neper y Bürgi, y posteriormente con la construcción de las primeras tablas de logaritmos en base 10, realizadas por H. Briggs (1631).

        Las tablas de logaritmos se fueron perfeccionando a través de los años, y fueron utilizadas en los cálculos y en la enseñanza hasta hace relativamente poco tiempo. La era de la computación fue haciendo que las tablas fueran más fáciles de elaborar, pero también las hizo innecesarias, pues ahora es más simple presionar un par de teclas en la calculadora, que buscar mantizas y características.

        Con el nacimiento del Cálculo Infinitesimal, las funciones exponencial y logarítmica comienzan a tener importancia desde un punto de vista teórico, al comenzar a ser estudiadas sus propiedades diferenciales. La importancia teórica de estas funciones ha invadido casi la totalidad de las áreas de la Matemática, sobre todo aquellas en que las nociones del cálculo diferencial e integral están presentes. Por otro lado, su importancia desde un punto de vista aplicado va mucho más allá de su uso en los cálculos numéricos. Estas funciones ya no se enseñan más como simple herramienta de cálculo numérico, sino como base de modelos sofisticados y poderosa herramienta teórica en diferentes áreas del quehacer científico.

Propiedades

    Las funciones logarítmicas de base a cumplen las siguientes propiedades:

• Son continuas en R_*⁺
• Pasan por (1;0) y (a;1)
• Si a>1 son crecientes y si 0<a<1 son decrecientes. Su crecimiento es menor que el de las funciones raíz de cualquier índice 
• La función logaritmica y la exponencial de la misma base son funciones inversas y por tanto sus gráficas son simétricas respecto de la recta y=x

Informacion obtenida de: http://www.ecured.cu/index.php/Funciones_logar%C3%ADtmicas#Definici.C3.B3n

Introduccion a las funciones algoritmicas

INTRODUCCIÓN

        La función logarítmica es  muy importante en matemáticas. Constituye un poderoso instrumento en la práctica del cálculo numérico. Por ser la recíproca de la exponencial, esta función es una de las de más presencia en los fenómenos observables . Así aparece en  la reproducción de una colonia de bacterias, la desintegración de una sustancia radiactiva, algunos crecimientos demográficos, la inflación, la capitalización de un dinero colocado a interés compuesto, etc.

Definición

El logaritmo de un número y es el exponente al cual hay que elevar la base b para obtener a y. Esto es, si b > 0 y b es diferente de cero, entonces:

log_b y = x si y sólo si y = b^x.

Nota: La notación log_b y = x se lee “el logaritmo de y en la base b es x”.

Función logarítmica

Sea a>0, (a ≠ 1), un número real. Se define la función logarítmica de base a como:

f: R_*⁺ → R

x → R

Dominio y rango de la función logarítmica

Sea f (x) = log _B x

  

   Dado que la función exponencial es la inversa de la función logarítmica, el rango de la función logarítmica es el dominio de la función exponencial, que es el conjunto de todos los números reales.

    El dominio de la función logarítmica es el rango de la función exponencial, dada por el intervalo (0, + infinito).

La informacion obtenida de:

http://www.ecured.cu/index.php/Funciones_logar%C3%ADtmicas#Definici.C3.B3n

http://www.analyzemath.com/spanish/logfunction/logfunction.html